Young diagrams

Partitionen sind umständlich zu handhaben: Es sind endliche (mitunter beträchtlich lange) Summen natürlicher Zahlen. Alle Summanden müssen festgehalten werden. Insbesondere das weitere Management mit Partitionen ist umständlich. Eine geradezu genial einfache Möglichkeit, Partitionen darzustellen, geht auf den Mathematiker Reverend Alfred Young zurück. Young definierte für jede Partition eine entsprechende graphische Darstellung. Gelegentlich heißen diese Young-Diagramme auch Ferrers Diagramme. Nehmen wir die beiden Zerlegungen der Zahl 15:

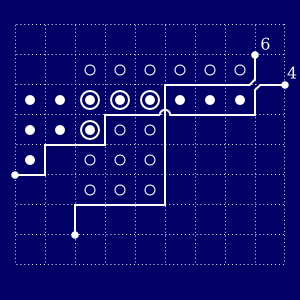
Alfred Young stellte die beiden Zerlegungen der Zahl 15 wie folgt graphisch dar:

Bei gleicher Anzahl der Quadrate in beiden Young Diagrammen ist deren äußere Gestalt zwar verschieden, beide Diagramme stehen jedoch in einer versteckten Beziehung zueinander. In welcher Beziehung? Man beachte die Konturen (shapes) der beiden Young Diagramme! Die Kontur eines Young Diagramms beschreibt dieses bereits vollständig (warum?). Daher gibt es eine ausgefeilte mathematische Theorie dieser Konturen. Diese beiden Young Diagramme zu den Zerlegungen der Zahl 15 heißen zueinander konjugiert. Jede der beiden Partitionen (und somit jedes der beiden Young Diagramme) zeichnet aber noch die zu suchende Eigenschaft aus. Man sammelt alle Partitionen mit der gleichen Eigenschaft in einer Klasse, es entstehen somit zwei Klassen. Das verblüffende Ergebnis: die beiden Klassen sind gleich groß, d.h. in ihnen liegen gleich viele Zerlegungen. Dies wiederum kann man durch eine leichte Manipulation der beiden Young Diagramme beweisen. Man kann die beiden Young Diagramme nämlich durch Spiegelungsabbildungen ineinander überführen.

Mit dieser Art der graphischen Darstellung einer Partition vermochte Alfred Young beachtliche Erfolge hinsichtlich der Entwicklung einer systematischen Theorie zu erzielen, die später von den Deutschen Mathematikern Issai Schur und dessen Schüler Georg Frobenius wesentlich erweitert werden konnte.

Auf diese Weise erschlug man zwei Fliegen mit einer Klappe: zum einen liefert die Darstellung einer Zerlegung in einem Young Diagramm in dem schier unübersehbar großen Wald der Partitionen auch nur einer einzigen Zahl Durchblick und Ordnung, zum anderen konnte man nunmehr leichter systematisch Ergebnisse erzielen und diese dann auf die bereits erwähnten Anwendungen übertragen. Dieser Prozess hält bis heute zu an.