| |
|
Algorithmische GRAPHENTHEORIE
in Theorie und Praxis
Workshop für Schüler der Klassen 7 bis 9
 Wie viele Farben benötigt man höchstens,
um die Länder auf einer Landkarte so zu färben, dass keine
zwei benachbarten Länder die gleiche Farbe haben? Gehört
die Lösung für dieses Problem zu demselben Gebiet der
Mathematik wie die Entwicklung eines Computerchips oder der Algorithmus,
nach dem ein Routenplaner arbeitet? Wie viele Farben benötigt man höchstens,
um die Länder auf einer Landkarte so zu färben, dass keine
zwei benachbarten Länder die gleiche Farbe haben? Gehört
die Lösung für dieses Problem zu demselben Gebiet der
Mathematik wie die Entwicklung eines Computerchips oder der Algorithmus,
nach dem ein Routenplaner arbeitet?
|
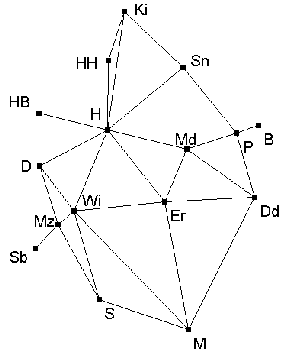 Nur wenige Gebiete der Mathematik sind derart weit
verzweigt wie das der Graphentheorie. Zum einen erfreut sich dieses
Gebiet allerhöchster Beliebtheit gerade bei auf Wirtschaftlichkeit
bedachten Anwendern. Durch eine zumeist einfache Abstraktion seines
Problems steht man schnell mitten im Sumpf dieser Theorie. Zuweilen
bringen relativ einfach erscheinende Fragestellungen gerade aus
der Graphentheorie Mathematiker schnell in Verlegenheit. Der berühmte
Vier-Farben-Satz, insbesondere sein Beweis, hat die Mathematiker
das Fürchten gelehrt. Nur wenige Gebiete der Mathematik sind derart weit
verzweigt wie das der Graphentheorie. Zum einen erfreut sich dieses
Gebiet allerhöchster Beliebtheit gerade bei auf Wirtschaftlichkeit
bedachten Anwendern. Durch eine zumeist einfache Abstraktion seines
Problems steht man schnell mitten im Sumpf dieser Theorie. Zuweilen
bringen relativ einfach erscheinende Fragestellungen gerade aus
der Graphentheorie Mathematiker schnell in Verlegenheit. Der berühmte
Vier-Farben-Satz, insbesondere sein Beweis, hat die Mathematiker
das Fürchten gelehrt.
Zum anderen zieht der Graphentheoretiker ganz unterschiedliche
mathematische Theorien, z.B. der Algebra, zur Lösung seiner
Probleme  heran. Ebenso unterschiedliche Situationen haben die Mathematik
um einige Spezialgraphen bereichert, die ihrerseits wiederum die
Entwicklung völlig neuartiger Ansätze erforderten. heran. Ebenso unterschiedliche Situationen haben die Mathematik
um einige Spezialgraphen bereichert, die ihrerseits wiederum die
Entwicklung völlig neuartiger Ansätze erforderten.
Dies macht die Beschäftigung mit Graphentheorie so spannend.
Als Folge dieser Umstände stellt sich die Graphentheorie jedoch
nicht als geschlossene, einheitliche Theorie dar, wie etwa die Lineare
Algebra oder die Analysis.
|
Als eines der jüngsten Gebiete der Mathematik
hat sie vielmehr die Aufgabe, für eine gegebene Anwendung nicht
einfach nur eine Lösung zu finden (wie in der Mathematik sonst
verbreitet), sondern insbesondere eine optimale Lösung. Typische
Fragestellungen sind: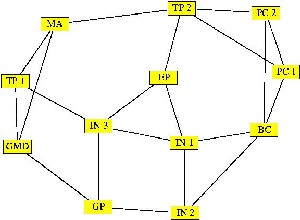
-
Wie kommt man am schnellsten von A
nach B?
-
Welche Mengen von welchen Waren können maximal von A nach
B gebracht werden?
-
Welche Ausgänge nimmt welcher Arbeiter in einem großen
Bürogebäude im Notfall, damit alles schnellst- und glattmöglichst
von der Bühne geht?
-
Welche Züge auf welchen Strecken setzt die Deutsche Bahn
ein, um möglichst kostengünstig alle Menschen zu ihrem
gewünschten Ziel zu bringen?
-
Wie baut die Regierung Autobahnen aus, um Staus auf besonders
beliebten Strecken zu vermeiden und die Fahrtzeiten zu optimieren?
-
Wie legt man mehr als 4 Meter Verdrahtungen auf einen noch
keine 4cm² großen Mikro-Chip, so dass die Signale alle
möglichst kurze Strecken zurücklegen, aber sich nicht
durch Induktion beeinträchtigen?
|
|
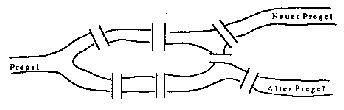 Man ahnt schnell: solche Aufgaben sind „mit
der Hand“ kaum zu bewältigen. Die Graphentheorie hilft
nicht nur bei der Konstruktion und Organisation moderner Elektronenrechner;
der Computer ist ebenfalls ein wesentliches Werkzeug zur Lösung
graphentheoretischer Probleme. Diese Wechsel- wirkung ist ein geradezu
typisches Merkmal heutigen Wissenschaftsmanagements in diesem Umfeld.
Die Informatik ist mit von der Partie: geeignete Datenstrukturen
und Algorithmen ermöglichen die Lösung von Problemen der
obigen Art in akzeptabler Zeit. (Die dazu benötigte Zeit zu
optimieren stellt ebenfalls ein großes Problem dar!) Man ahnt schnell: solche Aufgaben sind „mit
der Hand“ kaum zu bewältigen. Die Graphentheorie hilft
nicht nur bei der Konstruktion und Organisation moderner Elektronenrechner;
der Computer ist ebenfalls ein wesentliches Werkzeug zur Lösung
graphentheoretischer Probleme. Diese Wechsel- wirkung ist ein geradezu
typisches Merkmal heutigen Wissenschaftsmanagements in diesem Umfeld.
Die Informatik ist mit von der Partie: geeignete Datenstrukturen
und Algorithmen ermöglichen die Lösung von Problemen der
obigen Art in akzeptabler Zeit. (Die dazu benötigte Zeit zu
optimieren stellt ebenfalls ein großes Problem dar!)
|
|
 Die zentrale Rolle des Einsatzes von Computern in der Graphentheorie
erstaunt weniger als die einfach anmutende Tatsache, dass es in
der Graphentheorie zahlreiche Probleme gibt, die sich mit einem
Computer selbst schnellster Bauart (noch) nicht lösen lassen.
Davon weiß der Mathematiker Sebi Mänz ein Lied zu singen.
Sebi ist am Forschungsinstitut für DISKRETE MATHEMATIK an der
Universität Bonn mit der Entwicklung graphen- theoretischer Methoden
zur Herstellung optimal arbeitender und optimal organisierter Mikro-Chips
befasst. Die zentrale Rolle des Einsatzes von Computern in der Graphentheorie
erstaunt weniger als die einfach anmutende Tatsache, dass es in
der Graphentheorie zahlreiche Probleme gibt, die sich mit einem
Computer selbst schnellster Bauart (noch) nicht lösen lassen.
Davon weiß der Mathematiker Sebi Mänz ein Lied zu singen.
Sebi ist am Forschungsinstitut für DISKRETE MATHEMATIK an der
Universität Bonn mit der Entwicklung graphen- theoretischer Methoden
zur Herstellung optimal arbeitender und optimal organisierter Mikro-Chips
befasst.
Der Workshop soll einen Einblick in diese umfangreiche Theorie
geben. Gemeinsam werden wir Methoden zur Lösung von typischen
Problemen entwickeln und diese schrittweise verbessern.
Sebastian Mänz, Axel Bäuerle und Johannes Helmes leiten
den Workshop für Jugendliche der Klassen 7 bis 9 in Haus Eich.
|
| Wo |
Jugendbildungsstätte des Bistums
Aachen
Haus Eich
Eupener Straße 138
Aachen
|
| Wann |
Montag, 25.10.2004, Beginn 10:00
h
Freitag, 29.10.2004, Ende 17:00 h |
| Kosten |
420.00 EUR incl. aller Leistungen |
| Leistung |
Vollverpflegung (vier Mahlzeiten), an allen
Tagen jeweils ganztägiger Workshop |
| Anmeldung |
mit dem Anmeldeformular
können Sie sich verbindlich zu dem Workshop anmelden. Eine Anmeldung
nur per e-mail ist nicht möglich.
Das ausgefüllte Formular schicken Sie bitte per fax unter 02104 - 80
10 74 an das TMSZ oder mit gelber Post. |
| Bestätigung |
sobald sich die erforderliche Zahl der
TeilnehmerInnen angemeldet hat, erhalten Sie unser Bestätigungsschreiben. |
| Rückfragen |
bei Rückfragen stehen wir Ihnen gerne
telefonisch unter 02104-12 688 oder per e-mail zepf@fermat.de
zur Verfügung. |
 
|
|
|

 Wie viele Farben benötigt man höchstens,
um die Länder auf einer Landkarte so zu färben, dass keine
zwei benachbarten Länder die gleiche Farbe haben? Gehört
die Lösung für dieses Problem zu demselben Gebiet der
Mathematik wie die Entwicklung eines Computerchips oder der Algorithmus,
nach dem ein Routenplaner arbeitet?
Wie viele Farben benötigt man höchstens,
um die Länder auf einer Landkarte so zu färben, dass keine
zwei benachbarten Länder die gleiche Farbe haben? Gehört
die Lösung für dieses Problem zu demselben Gebiet der
Mathematik wie die Entwicklung eines Computerchips oder der Algorithmus,
nach dem ein Routenplaner arbeitet? Nur wenige Gebiete der Mathematik sind derart weit
verzweigt wie das der Graphentheorie. Zum einen erfreut sich dieses
Gebiet allerhöchster Beliebtheit gerade bei auf Wirtschaftlichkeit
bedachten Anwendern. Durch eine zumeist einfache Abstraktion seines
Problems steht man schnell mitten im Sumpf dieser Theorie. Zuweilen
bringen relativ einfach erscheinende Fragestellungen gerade aus
der Graphentheorie Mathematiker schnell in Verlegenheit. Der berühmte
Vier-Farben-Satz, insbesondere sein Beweis, hat die Mathematiker
das Fürchten gelehrt.
Nur wenige Gebiete der Mathematik sind derart weit
verzweigt wie das der Graphentheorie. Zum einen erfreut sich dieses
Gebiet allerhöchster Beliebtheit gerade bei auf Wirtschaftlichkeit
bedachten Anwendern. Durch eine zumeist einfache Abstraktion seines
Problems steht man schnell mitten im Sumpf dieser Theorie. Zuweilen
bringen relativ einfach erscheinende Fragestellungen gerade aus
der Graphentheorie Mathematiker schnell in Verlegenheit. Der berühmte
Vier-Farben-Satz, insbesondere sein Beweis, hat die Mathematiker
das Fürchten gelehrt. heran. Ebenso unterschiedliche Situationen haben die Mathematik
um einige Spezialgraphen bereichert, die ihrerseits wiederum die
Entwicklung völlig neuartiger Ansätze erforderten.
heran. Ebenso unterschiedliche Situationen haben die Mathematik
um einige Spezialgraphen bereichert, die ihrerseits wiederum die
Entwicklung völlig neuartiger Ansätze erforderten.
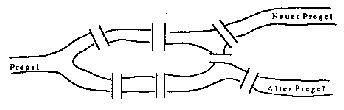 Man ahnt schnell: solche Aufgaben sind „mit
der Hand“ kaum zu bewältigen. Die Graphentheorie hilft
nicht nur bei der Konstruktion und Organisation moderner Elektronenrechner;
der Computer ist ebenfalls ein wesentliches Werkzeug zur Lösung
graphentheoretischer Probleme. Diese Wechsel- wirkung ist ein geradezu
typisches Merkmal heutigen Wissenschaftsmanagements in diesem Umfeld.
Die Informatik ist mit von der Partie: geeignete Datenstrukturen
und Algorithmen ermöglichen die Lösung von Problemen der
obigen Art in akzeptabler Zeit. (Die dazu benötigte Zeit zu
optimieren stellt ebenfalls ein großes Problem dar!)
Man ahnt schnell: solche Aufgaben sind „mit
der Hand“ kaum zu bewältigen. Die Graphentheorie hilft
nicht nur bei der Konstruktion und Organisation moderner Elektronenrechner;
der Computer ist ebenfalls ein wesentliches Werkzeug zur Lösung
graphentheoretischer Probleme. Diese Wechsel- wirkung ist ein geradezu
typisches Merkmal heutigen Wissenschaftsmanagements in diesem Umfeld.
Die Informatik ist mit von der Partie: geeignete Datenstrukturen
und Algorithmen ermöglichen die Lösung von Problemen der
obigen Art in akzeptabler Zeit. (Die dazu benötigte Zeit zu
optimieren stellt ebenfalls ein großes Problem dar!) Die zentrale Rolle des Einsatzes von Computern in der Graphentheorie
erstaunt weniger als die einfach anmutende Tatsache, dass es in
der Graphentheorie zahlreiche Probleme gibt, die sich mit einem
Computer selbst schnellster Bauart (noch) nicht lösen lassen.
Davon weiß der Mathematiker Sebi Mänz ein Lied zu singen.
Sebi ist am Forschungsinstitut für DISKRETE MATHEMATIK an der
Universität Bonn mit der Entwicklung graphen- theoretischer Methoden
zur Herstellung optimal arbeitender und optimal organisierter Mikro-Chips
befasst.
Die zentrale Rolle des Einsatzes von Computern in der Graphentheorie
erstaunt weniger als die einfach anmutende Tatsache, dass es in
der Graphentheorie zahlreiche Probleme gibt, die sich mit einem
Computer selbst schnellster Bauart (noch) nicht lösen lassen.
Davon weiß der Mathematiker Sebi Mänz ein Lied zu singen.
Sebi ist am Forschungsinstitut für DISKRETE MATHEMATIK an der
Universität Bonn mit der Entwicklung graphen- theoretischer Methoden
zur Herstellung optimal arbeitender und optimal organisierter Mikro-Chips
befasst.