Wir kennen es alle aus unseren teils unsäglichen Mathestunden: das bringe ich dann auf die rechte Seite, das auf die linke Seite, und dann teilen wir mal lustig durch x …. So oder ähnlich ist es abgelaufen, Generationen lang, und heute …. ?

Nun, wir haben ja schließlich und endlich Computer, die können das ja auch erledigen. - Wirklich? Können sie auch das? Das sog. Manipulieren von Formeln ist nun nicht gerade die erste Aufgabe eines Computers gewesen. Aus guten Grunde: zunächst standen nur sog. numerische Rechnungen auf dem Aufgabenplan eines Computers.

Inzwischen hat sich auch dies geändert, und zwar gewaltig. Computer beherrschen inzwischen auch das Manipulieren solcher Formeln. Das heißt nun nicht, dass man jede beliebige Formel eingeben könnte und der Computer "… löst die Sache mal soeben nach x auf " - Bingo.

Man muss sich allerdings schon eine Menge an Ideen einfallen lassen, wollte man mit den heutigen Tools einen Computer mit einer durch ihn nicht lösbaren Aufgabe dieser Art befassen.

C. Fasenmyer

Auch der Formelmanipulation liegt ein theoretisches Konzept zugrunde. Dieses Konzept wurde maßgeblich von der US-amerikanischen Mathematikerin, Sister Celine Fasenmyer, was die Grundlagen angeht, in ihrer Doktorarbeit entworfen. Interessant und hoch spannend ist dabei die Tatsache, dass dieses Konzept zu einer Zeit entstand, zu der niemand auch nur eine leiseste Ahnung davon hatte, von welcher Bedeutung diese Theorie sein würde, denn an die Implementierung auf einem Computer dachte zu dieser Zeit niemand. Inzwischen ist und wird diese Theorie ständig weiter ausgebaut. Tatsächlich lassen sich Spuren zurückverfolgen bis hin zu CFGauss, der sich mit hypergeometrischen Reihen befasste ohne zu wissen, dass auch diese Genossen eine grundlegende Rolle beim Thema symbolic computation spielen sollte.

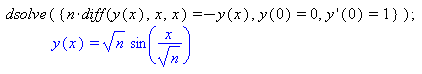
Was unseren Workshop angeht, so werden wir uns eine bestimmte Klasse recht komplizierter Formeln vornehmen, die der Computer aufgrund dieser Theorie auf eine nicht vorstellbare Weise vereinfachen kann, wobei man natürlich den Begriff "vereinfachen" noch formalisieren muss: was heisst es für eine Formel, einfacher zu sein als eine andere Formel? Tatsächlich gibt es auch hier ein Paradebeispiel einer harmlos erscheinenden Formel, die ein Computer bis heute mal nicht so eben vereinfachen kann. Woran das liegt, werden wir sehen. Professor Volker Strehl (Universität Erlangen-Nürnberg) ist ein international anerkannter Spezialist für derartige Fragestellungen, die heute unter dem Begriff symbolic summation firmieren. Die Österreichischen Mathematiker sind hier sehr fleißige Leute: das RISC (RISC = research institute for symbolic computation) in Linz/Donau ist weltweit eine federführende Einrichtung zu diesem Thema unter Professor Peter Paule.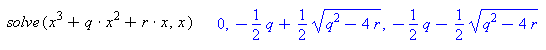

Schließlich zählt der Innsbrucker Mathematiker Bruno Buchberger zur Elite dieser Spezies. Der Hirte von der Alm entwickelte in seiner Promotion unter Wolfgang Gröbner den sog. Buchberger-Algorithmus, ohne den kein Formelmanipulator wie MAPLE, mu-math, Axiom oder MATHEMATICA überleben könnte. Seine Gröbnerbasen sind keine groben Tanten biblischen Ursprungs, sondern hoch leistungsfähige Konstrukte in dieser Welt des symbolischen Rechnens.

Werden wir etwas konkreter:

Nehmen Sie die Zahlen in einer beliebigen Zeile des wohlbekannten Pascal'schen Dreiecks. Die Summe dieser unter dem Namen Binomialkoeffizienten bekannten Zahlen innerhalb einer Zeile ergibt immer eine Potenz von 2. Das ist kein Zufall. Dies kann man recht einfach beweisen und liefert damit zugleich eine kombinatorische Fragestellung.

Kann ein Computer "diese Tatsache entdecken"? - Kann er, Sister Celine's Theorie und der nach ihr benannte Algorithmus können mehr: was denn nur, wenn jemand die Summe der Quadrate dieser Binomialkoeffizienten vereinfachen wollte, oder gar die Summe der Kuben ebendieser? Hier stoßen wir schon auf ein Problem: das kann Genosse C. eben nicht.

Carl Friedrich Gauss

Dem TMSZ liegt eine Sammlung von mehr als 600 solcher Summenformeln mit ausschließlich Binomialkoeffizienten vor, die allesamt mühsam von Hand bewiesen wurden. Heute kann man alle diese Summenausdrücke durch diesen Algorithmus der Sister Celine vereinfachen und damit auch noch zugleich beweisen. Das ist der weitere Gewinn dieser Theorie: Beweisen per Computer. Einige Gläubige springen hier sehr schnell auf die Tische: automatisches Beweisen? - Das lassen wir mal besser außen vor, um es mit CFGauss zu bezeichnen: pauca sed matura. (zwar weniger, das aber dann bitte richtig).