TMSZ
Numerische Mathematik - scientific computing
Fortpflanzungseigenschaften numerischer Fehler in Theorie und Praxis
Workshop für Schülerinnen und Schüler der Klassen 7 bis 9
|
Momentaufnahme I Herr Brechtel möchte eine Drainage in seinem Garten mit Kies auffüllen. Mit dem Zollstock bewaffnet notiert er sorgfältig die Maße seines ausgehobenen Kanals: (Tiefe, Breite, Länge) = (0.47 m, 0.39 m, 7,08 m). Nach dem Messen folgt das Rechnen: mit seinem Taschenrechner ermittelt er ein Netto-Volumen von genau 1,297764 m3. Dieses Volumen an Kies bestimmter Körnung bestellt Herr Brechtel bei der Baustoffgroßhandlung Böndgen. Für diese Art von Bestellung ist Herr Böndgen besonders sensibel. "Genauer konnten Sie dies nicht ermitteln?" - "Wie, noch genauer?" - "Herr Brechtel, bitte entscheiden Sie sich für einen oder für zwei Kubikmeter, wir zählen hier nicht die einzelnen Steinchen ab". Diese Situation kennzeichnet eine zentrale Fragestellung der sog. numerischen Mathematik. 
Jeder einigermaßen logisch denkender Mensch weiß, dass die Bestellangabe mit dieser Genauigkeit von 6 Dezimalstellen hinter dem Komma praktisch unbrauchbar ist. Was aber ist mit dem Argument … hat mein Taschenrechner aber errechnet ? Herr Brechtel ermittelt die jeweiligen Längen seiner Drainage mit einer Genauigkeit von jeweils 2 Dezimalstellen hinter dem Komma. Wenn dem schon so ist (soll heißen, dass diese drei Werte hinsichtlich ihrer Genauigkeit bereits erheblich in Zweifel zu ziehen sind!), so setzt Herr Brechtel dem noch eins drauf: mit nur 2-stelliger Genauigkeit erreicht er ein Ergebnis mit 6-stelliger Genauigkeit. - Es geht also um den Begriff der Genauigkeit. Nähme Herr Brechtel statt seiner drei Werte (Tiefe, Breite, Länge) = (0.47 m, 0.39 m, 7,08 m) jedoch die "ungenaueren" Werte (Tiefe, Breite, Länge) = (0.50 m, 0.40 m, 7,00 m) als Maße für sein Vorhaben, so erhielt er ein Volumen von 1,4 m3. Der Ersatz der Werte 0.47, 0.39 und 7.08 durch die Werte 0.5, 0.4 und 7,0 bedeutet einen Verzicht an (vermeintlicher Brechtel-) Genauigkeit mit der Folge, dass Herr Brechtel bei seiner Bestellung von 1,4 m3 Kies nun nicht mehr so ganz daneben liegen dürfte. - Hat Herr Brechtel mit seinen Messwerten wirklich so ganz daneben gelegen? Wer weiß das denn? Wann kann man sagen: diese Zahl ist das wahre Volumen des Kanals? Gibt es dieses wahre Volumen überhaupt? Halten wir fest: beim Rechnen mit Dezimalzahlen (numerische Mathematik!) können wir nicht "einfach drauf los rechnen" und die jeweiligen Ergebnisse ohne jede weitere Betrachtung als "wahre", d.h. gültige Zahlen hinnehmen, auch wenn diese durch einen noch so funktionstüchtigen Rechner korrekt ermittelt wurden! In dem (numerischen) Sinne sind die Ergebnisse eben nicht korrekt, d.h. über mehr Stellen, als die die "am wenigsten genaue" Zahl Stellen hinter dem Komma enthält, können wir letztlich nichts aussagen. Auch hier gilt: die Kette ist so stark wie das schwächste Glied.
Momentaufnahme II Empört beklagt sich Kevin bei seiner LK-Englischlehrerin: sie habe einen englischsprachigen Ausdruck als Fehler bewertet, obwohl seine Version sprachlich auch möglich sei. Das wisse er schließlich von seinem Aufenthalt in den USA ziemlich genau. Die Lehrerin nimmt souverän den Fehler mit dem Ausdruck des tiefsten Bedauerns zurück und korrigiert die Gesamtfehlerzahl artig um 1 nach unten. Kevin besteht natürlich darauf, dass nunmehr bitte schön auch die Gesamtnote zu korrigieren sei. "Kevin - bitte - noch nichts vom Fehlerfortpflanzungsgesetz embryonaler Grammatikfehler eines adulten Kevins gehört, mein lieber." - . - Ja, ja, schon gut . - . - NO COMMENT.
In unserem Workshop befassen wir uns mit der Frage, wie sich Fehler (Messfehler, Rechenfehler, Grammatikfehler, etc.) auf das Ergebnis in sich anschließenden Rechnungen auswirkt. Diese Frage ist von zentraler Bedeutung für mathematische Anwendungen. Fehler in Eingangsgrößen können sich aufschaukeln und mitunter verheerende Folgen in weiteren Rechnungen nach sich ziehen; Fehler in Eingangsgrößen können sich aber auch gegenseitig kompensieren und möglicherweise sogar aufheben. Wann was geschieht, hängt u.a. von den Rechnungen (Additionen, Subtraktionen, Divisionen, etc…) ab. Der Division kommt hierbei besondere Aufmerksamkeit zu, denn gerade sie lässt gelegentlich die Puppen tanzen und sorgt für mathematische up's and down's. Der Mathematiker Rutishauser hat hierfür ein schönes Beispiel angegeben: er veränderte an einem eigens zu diesem Zweck konstruiertes Gleichungssystem mit 30 Unbekannten nur einen einzigen Koeffizienten auf der fünften Stelle hinter dem Komma und mit einem mal veränderte sich die komplette Lösung des Gleichungssystems. Der Mathematiker Wilkinson hat gezeigt, wie sich sog. Polynome verhalten, wenn nur schon zwei ihrer Nullstellen extrem nahe beieinander liegen: sie schaukeln sich derart auf, dass sie nicht mehr beherrschbar erscheinen. Nicht zu reden von sog. Nullstellenhaufen. Auf solche (in Anwendungen häufig vorkommende) Situationen ist man jedoch gefasst.
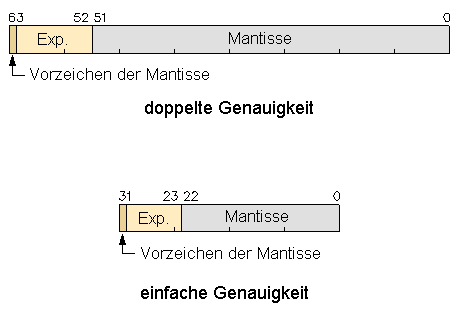
Uns allen ist der sog. Rundungsfehler langläufig bekannt. Die Arbeitsweise jeden Computers basiert konstruktionsbedingt auf sog. numerischen Fehlern: die Register eines jeden Computers verfügen nur über endlich viele Bitstellen. Wenn alle Bitstellen signifikant besetzt sind, dann entstehen bei weiteren Rechnungen mit diesen Zahlen zwangsläufig numerische Fehler, die sich zwar auf Stellen hinter der letzten Bitstelle auswirken, die man aber deshalb nicht einfach unter den Tisch fallen lassen kann. Diese Situation kann man plausibel so beschreiben: der Computer betrachtet zwei (verschiedenene!) Zahlen als gleich, wenn sie sich um weniger unterscheiden, als seine Arithmetik es zulässt. Das klingt zwar einleuchtend, hat aber erhebliche Auswirkungen für das Rechnen mit derartigen Zahlen. Deshalb hat man sich eine Menge Gedanken darüber gemacht, wie man diese Klippen (innerhalb weiterer Grenzen) umschiffen kann: Gleitkomma-Arithmetik. Aber auch diese Akrobatik hat letztlich ihre Grenzen. Jede numerische Rechnung (neben diesen gibt es auch andere Rechenarten wie z.B. symbolisches Rechnen) auf einem Computer vollzieht sich innerhalb endlicher Rechenräume. Da hilft auch kein Ruf nach Computern mit größerer Registerlänge. Die ALU (arithmetic and logical unit) im Prozessor des Computers kann grundsätzlich nur eine begrenzte und damit endliche Anzahl an Ziffern (im Dualsystem sind es die Bitstellen) verarbeiten. Aus dieser Klemme finden die Mathematiker immer noch ein Schlupfloch: man kann eine beliebig lange Bitstellenarithmetik quasi simulieren, d. h. die Mathematiker schaffen neue Dimensionen von Genauigkeit, indem sie Zahlen mit mehr Ziffern als das Rechenregister aufnehmen kann wie mit einer Lupe portionsweise scannen (sliding window technique). Die dabei entstehenden "versteckten" Rechenaufwände sind bei der Aufwandsberechnung hochgenauer Zahlen zu beachten. Neben derlei Überlegungen ist es eine weitere Aufgabe der numerischen Mathematik, für komplizierte oder sehr aufwendig zu berechnende Funktionen sog. Ersatzfunktionen zu entwickeln, die eine "hinreichende" Genauigkeit besitzen oder eben wesentlich weniger aufwendig zu berechnen sind. Die Klasse der Polynome spielt hierbei eine besondere Rolle: wir stoßen auf Lagrange-Polynome, Laguerre-Polynome, Newton-Polynome, Hermite- Polynome, Tschebycheff-Polynome. Allein die Namen verraten, dass derartige Methoden schon sehr früh entwickelt wurden zu einer Zeit, als man nicht einmal das Wort Computer kannte. Jeder, der die Taste zur Berechnung der Wurzel(2) betätigt, löst den Start eines Mikroprogramms aus, das zur Berechnung der Wurzel(2) eine höchst einfach zu berechnende Ersatzfunktion heranzieht. Ebenso verhält es sich mit der Berechnung von Funktionen wie sin(x), tan(x), sec(x) und deren co-Funktionen. Als unverzichtbarer Bestandteil dieser Thematik werden wir uns intensiv mit der Datendarstellung der Dezimalzahlen beschäftigen. Diese Darstellung ist auch Thema bei der Betrachtung der Fortpflanzung von Fehlern. Dabei schleicht sich die Frage nach der Umwandlung von Dezimalzahlen in Dualzahlen (mit Stellen hinter dem Komma!) ein: 1001101,010012 als Dualzahl verstanden!!! Bereits bei der Umwandlung von Dezimal- in Dualzahlen sind mögliche Fehler zu vermeiden, denn diese Fehler sind computerintern entstanden und gehören daher in die Verantwortung der Rechnerhersteller. 
Gerade für Anwendungen ist die Interpolation von höchster Bedeutung: hat man eine Liste von Funktionswerten, unter denen jedoch ein gesuchter Funktionswert nicht vorkommt, so muss man einen Funktionswert aus den Daten der Wertetabelle ermitteln: hierzu gibt es verschieden Verfahren, solche Zwischenwerte eigenhändig mit einer vorgegebenen Genauigkeit zu ermitteln. Für ein zentrales Problem sorgen Zahlen vom Typ der Kreiszahl π = 3.14159….. Ihre grenzenlose Genauigkeit lässt jeden Gedanken an eine genaue Darstellung dieser (und unendlich vieler anderer Zahlen dieses Typs) blass erscheinen. Numerisch kann man mit π = 3.14159…. nur näherungsweise rechnen. Wie ist es möglich, die Zahl π auf zig Millionen Stellen hinter dem Komma genau zu ermitteln, wenn doch der Computer nur 32 Bitstellen hat? Eine elegante Technik stellt die sog. Intervallarithmetik dar: an Stelle einzelner Zahlen betrachtet man definierte Intervalle, mit denen man Rechnen kann. Die Operanden sind nicht mehr Zahlen, sondern Intervalle (Zahlenmengen). Es entsteht eine Intervallalgebra mit ähnlichen Gesetzen wie wir sie vom Rechnen mit einzelnen Zahlen kennen. Jede Zahl kann man mit einem Intervall versehen. Nun rechnet man an Stelle mit einzelnen Zahlen mit dem ganzen Intervall, in dem sie liegt. Der Effekt: als Ergebnis liefert die Intervallrechnung ein Intervall, in dem auch das sonst einzeln berechnete Ergebnis liegt mit dem Vorteil, dass diese eine Rechnung (mit Intervallen) nun für alle Zahlen gilt, die in den betrachteten Intervallen liegen. |
| Wo |
Jugendakademie Haus Venusberg
Haager Weg 28-30, 53127 Bonn-Venusberg |
| Wann |
Montag, 09.04.2007, Beginn 10:00 h
Freitag, 13.04.2006, Ende 17:00 h |
| Kosten | 420.00 EUR incl. aller Leistungen |
| Leistung | Vollverpflegung (vier Mahlzeiten), an allen Tagen jeweils ganztägiger Workshop |
| Anmeldung |
mit dem Anmeldeformular
können Sie sich verbindlich zu dem Workshop anmelden. Eine Anmeldung nur per e-mail ist nicht möglich. Anmeldeschluss ist der . Das ausgefüllte Formular schicken Sie bitte per fax unter 02104 - 80 10 74 an das TMSZ oder mit gelber Post. |
| Bestätigung | Sobald sich die erforderliche Zahl der TeilnehmerInnen angemeldet hat, erhalten Sie unser Bestätigungsschreiben. |
| Rückfragen | bei Rückfragen stehen wir Ihnen gerne telefonisch unter 02104-12 688 oder per e-mail zepf@fermat.de zur Verfügung. |